Control Structures
Making Decisions: if
We are going to have to start writing code that makes decisions based on the result of calculations, user input, … .
e.g. from our guessing game: If they say your guess is too small, the smallest possible number is now the guess plus one.
Sometimes we'll pass that instruction and change the smallest number
, but sometimes not.
Making Decisions: if
The most common way to make decisions is the if
statement.
The idea: our code will be structured like this:
if [this is true]:
[do this stuff but
otherwise skip it]
Making Decisions: if
Some actual code using an if:
num = int(input("Enter ten: "))
if num == 10:
print("Well done.")
print("Thanks for trying.")
It might do this (if the user actually types 10
):
Enter ten: 10 Well done. Thanks for trying.
Or this:
Enter ten: 12 Thanks for trying.
Making Decisions: if
In Python, the indented code after the if is only executed when the condition is true
if [condition]:
[Executed if the condition
evaluated to
true.]
[This code is executed next, no
matter what.]
Everything in the body of the if must be indented the same amount: 4 spaces by convention.
Conditions
The condition for the if is how the decision is made.
It's a boolean expression: an expression that evaluates to either true or false.
Boolean values are another Python type (like integers, floating point, strings). There are only two: True and False.
Conditions
Some boolean operators (i.e. operators that when evaluated result in a boolean value):
| Operator | Name/operation |
|---|---|
== | is equal to |
!= | not equal to |
< | less than |
<= | less than or equal |
> | greater than |
>= | greater than or equal |
Conditions
Boolean expressions can be used anywhere but are especially useful as the if condition.
>>> 10 == 9 False >>> 10 > 9 True
Conditions
= vs ==:
The = is for variable assignment: the thing of the left must be a variable name. The variable is updated but no value is returned
.
The == is for making comparisons: it forms an expression that returns True or False.
If/Else
It's often useful to have an otherwise
case for an if
. i.e. if the condition is true, do X, but if it was false, do Y.
If/Else
An else
clause can be used for this. The structure:
if [condition]:
[Executed if the condition
evaluated to true.]
else:
[Executed if the condition
evaluated to false.]
[This code is executed next, no
matter what.]
The else clause can be included on any if, but it's not required.
If/Else
Let's expand the last example:
num = int(input("Enter ten: "))
if num == 10:
print("Well done.")
else:
print("No!")
print("Thanks for trying.")
Now, two runs of this program:
Enter ten: 10 Well done. Thanks for trying.
Enter ten: 12 No! Thanks for trying.
If/Elif/Else
If if/else structure lets you handle a situation where there are two outcomes (the condition evaluates to either True or False). e.g. some kind of right
or wrong
decision.
If you have a multi-way decision to make, adding one or more elif clauses to handle it… .
If/Elif/Else
The structure:
if [condition 1]:
[Executed if condition 1 is true.]
elif [condition 2]:
[Executed if condition 1 was false but
condition 2 is true.]
else:
[Executed if neither condition 1 nor
condition 2 were true.]
[This code is executed next, no
matter what.]
If/Elif/Else
So, we could write something like this:
num = int(input("Enter ten: "))
if num == 10:
print("Well done.")
elif num > 10:
print("Too big.")
else:
print("Too small.")
The else will be executed if none of the above conditions was true. e.g. in this case, that will be when num<10.
If/Elif/Else
More elif blocks can be added to represent as many cases as you need to handle.
if num == 10:
print("Well done.")
elif num > 100:
print("Much too big.")
elif num > 10:
print("Too big.")
else:
print("Too small.")
Only the first block where the condition is true will run. e.g. if the user enters 110, the num>100 case will run but not the num>10 code.
Intersecting Lines
We have enough tools now to solve a real
problem. This is (just an) example of going from problem → algorithm → program.
The problem: the user describes two lines by giving two \((x,y)\) points on each line. We have to tell them if the lines are parallel, or if they intersect, where?
Intersecting Lines
e.g. in this scenario, we would like to find the intersection at (what looks like) \((2, 1)\).

Intersecting Lines
First, some prelimiary work. It's always a good idea to think and know how to actually sold be problem before starting to type.
For line A
with points \((x_1,y_1)\) and \((x_2,y_2)\), and a line B
on points \((x_3,y_3)\) and \((x_4,y_4)\), they have slope and intercepts,
Intersecting Lines
Then, they intersect at,
\[\begin{align*} m_A x + b_A &= m_B x + b_B \\ (m_A - m_B)x &= b_B - b_A \\ x &= -\frac{b_B - b_A}{m_B - m_A}\,,\\ y &= m_A x + b_A\,. \end{align*}\]Intersecting Lines
In our program, we will need to get the input:
x1 = float(input("Enter x1: "))
y1 = float(input("Enter y1: "))
x2 = float(input("Enter x2: "))
y2 = float(input("Enter y2: "))
x3 = float(input("Enter x3: "))
y3 = float(input("Enter y3: "))
x4 = float(input("Enter x4: "))
y4 = float(input("Enter y4: "))
Intersecting Lines
Then:
- We can calculate the intercept with the formulas above.
- … unless the lines are parallel.
- … or identical.
- … or if one or both are vertical.
Intersecting Lines
Let's try it.
My plan: deal with all cases except vertical lines.
Intersecting Lines
Aside: this marks the point where you have all of the tools necessary to do assignment 1, but some practice provided by the exercises 2 and 3 might help you get started.
Repetition
We need to be able to repeat pieces of code. e.g. do the same operation on all of the values in a list, or search until we find something, etc.
Repetition
Repetition generally falls into one of two categories…
- You know at the start how many times you'll repeat, like iterating through a list (where you know the list has 10 things). That's definite iteration.
- You don't know when to stop, but will when you see it, like searching for something. This is indefinite iteration.
The for Loop
The for loop in Python will give us a tool for definite iteration: when we know when we start how many repetitions we need.
The for Loop
A simple example: count from 1 up to a number the user enters:
n = int(input("Count how high? "))
for i in range(n):
print(i+1)
The for loop iterates through the collection it's give (range(n) here). It runs the body of the loop (the print statement) once for each value, setting the loop counter (i) each time.
The for Loop
n = int(input("Count how high? "))
for i in range(n):
print(i+1)
The range(n) function call gives a collection of values from 0 to n-1: I wanted to count from 1 to n so I added one to i each time.
The for Loop
Another way we could have counted from 1 to n: if we give range two arguments, they are the start and one-past-last:
for i in range(1, n+1):
print(i)
The for Loop
The variable after the
is the index variable or loop index.for
It can be named anything, and will be set to the next value for each execution of the loop body. Then it can be used just like any other variable (or ignored if you don't need it).
The for Loop
Another example: we want to sum several numbers. I want output like this:
How many numbers? 4 Enter value 1: 1.2 Enter value 2: 3 Enter value 3: 4.56 Enter value 4: 7.8 The total is 16.56
The for Loop
This will be one of the first times we have used a variable that actually varies: we will keep a running total of the numbers as we see them. The total will start at zero.
num = int(input("How many numbers? "))
total = 0.0
Then we'll have to fill in the loop. At the end, we can report the total:
print("The total is " + str(total))
The for Loop
We know we're going to have to loop num times:
for pos in range(num):
The for Loop
In the loop, we need to ask for the next value, and add it to the running total:
for pos in range(num):
value = float(input("Enter value " + str(pos+1) + ": "))
total = total + value
The for Loop
All together:
num = int(input("How many numbers? "))
total = 0.0
for pos in range(num):
value = float(input("Enter value " + str(pos+1) + ": "))
total = total + value
print("The total is " + str(total))
The while Loop
The for loop gave us a tool for definite iteration: we decided on the size of the range at the start of the loop, then iterated that many times.
The while loop will give us a way to do inefinite iteration: we'll keep looping until we decide
we're done.
The while Loop
Just like with a if block, a condition will be how we make the decision. A while loop actually looks a lot like an if, but the behaviour is keep doing this until the condition becomes
False.
The while Loop
A simple example:
n = 1
while n < 10:
n = n * 2
print(n)
print("Done.")
As the loop starts: check the condition (n<10) and if it's True, run the loop body. Then check the condition again and if it's True, run it again. Eventually (we hope) the condition will evaluate to False and the loop exits.
The while Loop
n = 1
while n < 10:
n = n * 2
print(n)
print("Done.")
The output of this code:
2 4 8 16 Done.
The while Loop
We can implement a simple add up some numbers
program, but without asking the user for the count at the start:
Enter numbers, 0 to stop. Enter a number: 10 Enter a number: 20 Enter a number: 30 Enter a number: 0 The total is 60.0
We want the loop to exit after the user enters zero.
The while Loop
Attempt #1:
print("Enter numbers, 0 to stop.")
total = 0.0
while val != 0.0:
val = float(input("Enter a number: "))
total = total + val
print("The total is " + str(total))
Close, but what's the problem?
The while Loop
The first time the loop condition is evaluated, the variable val hasn't been set yet, so it doesn't exist.
print("Enter numbers, 0 to stop.")
total = 0.0
while val != 0.0:
That causes:
NameError: name 'val' is not defined.
The while Loop
There are a few ways to deal with that, but what I'd actually do: set it to a dummy value (anything but zero) so we get into the loop correctly on the first iteration):
print("Enter numbers, 0 to stop.")
total = 0.0
val = 1.0 # dummy value so we enter the loop
while val != 0.0:
val = float(input("Enter a number: "))
total += val
print("The total is " + str(total))
The while Loop
val = 1.0 # dummy value so we enter the loop
That's also the first time I have used a comment: anything after a # on a line is ignored by Python. It can (and should) be used to leave human-readable explanation of tricky parts.
The while Loop
When a program gets to the start of a while loop:
- Evaluate the condition. If it's
False, skip to #4. - Run all of the loop body.
- Go back to #1.
- Run the code after the loop body.
The while Loop
Something about the while loop condition have better make the condition False eventually, otherwise the program will loop forever.
Press ctrl-C to stop a runaway program. (It's going to happen eventually.)
If the condition is False right away, the loop body will run zero times.
The while Loop
So if you want to use a while loop, you need to figure out some condition that will tell you when you should continue: how do you know you should keep going around the loop (vs exit and move on)? That's the while condition.
And figure out how to do one step
: what do you need to do as one iteration of your algorithm
? That's the loop body.
The Guessing Game
We now have all the pieces we need to implement the guessing game. (Slightly modified pseudocode.)
- Tell the user to pick a number between 1 and 100.
- The smallest possible number is 1; the largest is 100.
- Until we guess correctly…
- Guess \(\lfloor(\mathit{smallest} + \mathit{largest}) / 2\rfloor\).
- Ask if their number is smaller, larger, or equal.
- If they say it's equal, the game is over.
- If they say it's larger, the smallest possible number is now the guess plus one.
- If they say it's smaller, the largest possible number is now the guess minus one.
The Guessing Game
Some decisions we have to make:
- What variables do we need (and what should they store)?
- Which loop structure (
fororwhile)? - How do we deal with the input and decide if we're done?
Example: special numbers
Suppose you have a function is_special(n) that can tell you whether a number is special
or not. (The definition of special
doesn't really matter, as long as you know that some numbers are and some aren't.)
We'll use a pre-prepared definition of the function (in special.py). Then we can use it (in a .py file in the same folder) like this: (More later: modules
)
from special import is_special
Example: special numbers
We'll ask the user to enter num (an integer). Which loop would you use to…
- print the first
numspecial numbers? - print out all special numbers between
1andnum?
Running Time
As soon as we start writing loops, our programs can run for a long time. We should design algorithms that can be completed in a reasonable amount of time.
There are two issues here: the algorithm itself and the way we implement it in code.
Running Time
e.g. our guessing game could have been much slower. This would be a much worse algorithm/program.
- Tell the user to pick a number between 1 and 100.
- The guess is 1.
- Until we guess correctly…
- Guess.
- Ask if their number is smaller, larger, or equal.
- If they say it's equal, the game is over.
- Add one to the guess.
i.e. guess 1, 2, 3, … until we get it right.
Running Time
We need some way to measure how long an algorithm will take: a way to quantify how that guessing game is worse than our original.
One possibility: just count the number of steps
needed to finish: up to 100 for that game, but at most 7 for the original.
Running Time
The problem: that doesn't tell me anything about how it changes as the problem grows/shrinks. e.g. what if it was between 1 and 100000
or between 1 and 3
?
Running Time
What we're going to do: count the number of steps
, depending on the size of the problem. Step ≈ number of times we run through a loop.
We'll look at the worst-case running time: the maximum number of steps it can take to finish.
Of course, in the guessing game, we might get lucky on the first guess, but that's somehow not very interesting.
Running Time
The number of steps
will depend on the size of the problem, usually denoted \(n\). e.g. for the guessing game, we have been using \(n=100\), but other sizes are obviously possible.
The slow guessing game takes at most \(n\) steps, but what about the original one?
Running Time
The guessing game started with 100 possible values, then 50, then 25, then ∼12, … . At worst, we might not guess correctly until there's only one possibility left.
How many is that in general? The number of possibilities after each guess is, \[ n \rightarrow \tfrac{n}{2} \rightarrow \tfrac{n}{4} \rightarrow \tfrac{n}{8} \rightarrow\cdots\rightarrow \tfrac{n}{2^k}=1\,. \]
It stops after \(k\) steps (worst case) when \(\frac{n}{2^k} = 1\) or \(k=\log_2 n\).
Running Time
The \(\log_2 n\) function grows very slowly, so this game is very fast, even for a large maximum number.
| \(n\) | \(\log_2 n\) |
|---|---|
| 128 | 7 |
| 1024 | 10 |
| 1048576 | 20 |
| 109 | ≈30 |
Running Time
Consider another problem: given a string, check to see if there are any repeated characters.
e.g. for "CMPT" we want to say no; for "MACM" we want to say yes because there are two Ms.
Running Time
An algorithm we could use for that:
- Set the counter to 0.
- For each letter in the string,
- For each letter after that letter,
- If the two are the same, add 1 to the counter.
- For each letter after that letter,
- If the counter is 0, say no. Else say yes.
Running Time
For a string with \(n\) characters, the innermost step (If the two…
) runs \(n-1\) times for the first letter, then \(n-2\) for the second, \(n-3\) for the third, … . Because of something I remember from a math class, the total steps is: \[\frac{n(n-1)}{2} = \tfrac{1}{2}n^2 - \tfrac{1}{2}n\,.\]
Running Time
When looking at running times, we generally only worry about the fastest-growing terms: the largest power of \(n\) (or other rules later).
So, we think of \(\tfrac{1}{2}n^2 - \tfrac{1}{2}n\) steps as just \(\tfrac{1}{2}n^2\).
Running Time
We also will ignore the leading constant: the rough analysis we have done doesn't really say much about the kind of efficiencies that can make a real implementation (program) run a few times faster/slower. We're fooling ourselves if we keep those constant factors.
So, \(\tfrac{1}{2}n^2\) becomes \(n^2\) and we say this repeated letters algorithm has \(n^2\) running time
Running Time
The overall formula for the number of steps tells us a lot about the time an algorithm will take. Some common ones:
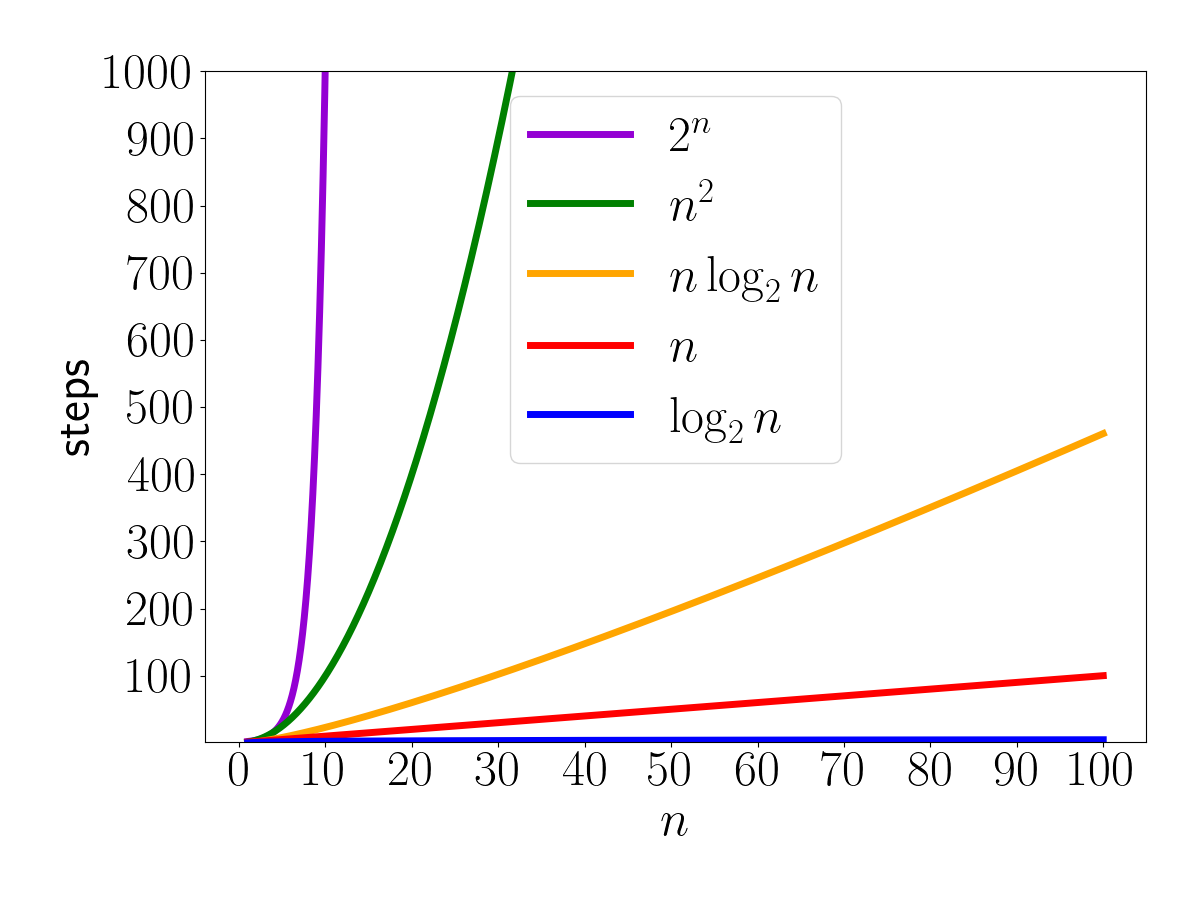
Running Time

You can see the reason we throw away slower-growing terms when talking about running time: they make a relatively tiny contribution to the total with a larger \(n\). We imagine solving small
problems is easy and we're more concerned about large
cases.
Running Time
The actual rules for coming up with a running time
:
- Count the number of
steps
taken to run the algorithm with asize \(n\)
input. - Throw away all but the fastest-growing term.
- Throw away any constant factor.
Running Time
Some possible fastest-growing terms
, in order from fastest growing to slowest growing:
Or in short: think of \(2^n\) as \(n^{1000000}\) and \(\log n\) as \(n^{0.0000001}\) and just think about the power of \(n\).
Running Time
So far, we have seen algorithms with these running times:
- the
good
guessing game: \(\log n\), - the
bad
guessing game: \(n\), - detect repeated letters: \(n^2\).
Running Time
One last problem: given a list of numbers, can we find some of them that add to a particular total?
e.g. given values 6, 14, 127, 7, 2, 8, can we find a subset that add to 16? In this case yes: 6, 2, 8.
Running Time
The best algorithm for this (that I can think of):
- For every subset of the list,
- Add up the values in that subset
- If the sum == the target,
- Print the subset.
There are \(2^n\) subsets, so this algorithm has running time \(2^n\)
.
Running Time
A running time of \(2^n\) is really bad: \(2^{30} \approx 10^9\). We probably couldn't practically solve this problem for sets of more than 30 or 40 values.
If the best algorithm we can think of has exponential running time, in some sense we don't really have a solution: it's too slow for all but the smallest cases. Unfortunately, that's the case for many interesting problems.
Running Time
Aside for the more mathematically inclined: we're saying an algorithm has running time \(f(n)\)
if the formula for its running time is both \(O(f(n))\) and \(\Omega(f(n))\).
Running Time
Why are we looking at running times? It seems imprecise.
It's a measurement of how fast an algorithm is, ignoring the specific implementation. A clever program/implementation might be able to turn \(3n^2\) steps into \(2n^2\) steps (and thus maybe 300 ms to 200 ms on some specific input), but getting to \(n\log n\) takes a different algorithm and that will always do better for large enough \(n\).
Running Time
At the same time, a clever programmer can often create a much faster implementation of the same algorithm. (e.g. I have examples in other courses with 100× speed differences because of more clever programming.)
Too many inexperienced programmers ignore the algorithm. Too many computer scientists ignore the importance of an efficient implementation.
Running Time
Finding repeated letters can actually be done with running time \(n\log n\).
Hint: sorting \(n\) values can be done in \(n\log n\) steps.
Running Time
That implies an algorithm like this:
- Sort the characters in the string.
- Set the counter to 0.
- For every character except the last,
- Compare the character with the one after it.
- If they are the same, add 1 to the counter.
- If the counter is 0, say no. Else say yes.
The sort the characters
operation implies \(n\log n\) steps; the rest of the algorithm takes \(n\) steps. The running time is \(n\log n + n\) which is simplified to \(n\log n\).