Representing Information

We have seen that computers (specifically with Python) can store different types of information.

Let's look a little a how they do that.

Bits and Bytes

The fundamental problem: computers themselves only store or transmit bits. That is, values that can either be 0 or 1 (or on/off or true/false or up/down or whatever you want to call them). That's true in the computer's memory (RAM), storage (disks, USB storage, etc), over the network, … .

So then how do computers deal with anything else?

Bits and Bytes

Usually, a single bit is too small a unit of information to work with: multiple bits make more sense. Eight bits is one byte. These are four bytes:

00001101 11001011 00000000 11111111

There are \(2^8 = 256\) different bytes.

Usually a bit is signified by a b and byte by B. (Not everybody is consistent with that, but we will be.)

Bits and Bytes

The metric prefixes kilo (k), mega (M), giga (G) are used when describing bits or bytes.

But usually, factors of \(2^{10} = 1024\) are used instead of \(1000\): it's often more convenient to work with power of two.

Bits and Bytes

Usually we would say:

Prefix	Usual computer-related meaning
k	\(2^{10} = 1024\)
M	\(2^{20} = 1048576\)
G	\(2^{30} = 1073741824\)

So, 5 MB = 5 × 1048576 × 8 = 41943040 bits.

If you have a computer with 16 GB of memory, that's 137,438,953,472 bits.

Integers

So your computer can store/manipulate a lot of bits. Great, but we still need to do something useful with them.

First thing we can do: represent integers. Specifially (for now), unsigned integers (so no negative values, only 0 and up).

Integers

At some point, somebody taught you about positional numbers:

\[\begin{align*} 345 &= (3\times 100) + (4\times 10) + 5 \\ &= (3\times 10^2) + (4\times 10^1) + (5\times 10^0)\,. \end{align*}\]

Integers

We usually count in decimal or base 10: there are ten values (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) that can go in each position. Moving left a position increases the value by a factor of 10.

e.g. if we add a zero to the right of 345 to get 3450, the value is ten times larger.

Integers

We can do all the same positional number stuff, but with two instead of ten:

\[\begin{align*} 1001_2 &= (1\times 2^3) + (0\times 2^2) + (0\times 2^1) + (1\times 2^0) \\ &= 8 + 1 \\ &= 9\,. \end{align*}\]

Then we can represent these things with bits. These are base 2 or binary numbers.

Integers

Unless it's completely clear, we should label values with their base as a subscript so they aren't ambiguous.

\[\begin{align*} 1001_2 &= (1\times 2^3) + (0\times 2^2) + (0\times 2^1) + (1\times 2^0) \,, \\ 1001_{10} &= (1\times 10^3) + (0\times 10^2) + (0\times 10^1) + (1\times 10^0) \,. \end{align*}\]

e.g. on the left, 1001 could be any base. On the right, math is pretty much always in base 10.

Integers

When we're storing these in a computer, we generally have to decide how many bits are allocated to each value. e.g. computers don't generally work with integers but rather 8-bit integers (or some other size).

If we wanted to represent \(9_{10}\) as an 8-bit integer, it would be \(00001001_{2}\).

Integers

So 8-bit integers have these positional values:

Integers

That means there is a smallest and largest number that can be represented. The smallest will be zero: all 0 bits.

The largest will be all 1 bits. For 8-bit values, that's: \[2^7 + 2^6 + \cdots + 2^1 + 2^0 = 2^8-1 = 255\]

In general, \(n\) bits store unsigned integers 0 to \(2^n-1\).

Integers

For real calculations, 64-bit integers are more common, giving a range 0 to \[2^{64} - 1 = 18446744073709551615\,.\]

Python works with 64-bit integers, but it hides the limitation from us.

>>> 18446744073709551615 + 1
18446744073709551616
>>> 18446744073709551615 * 2
36893488147419103230

Adding Integers

Addition (and other basic arithmetic operations) work basically the same as base 10. You should be able to add decimal numbers:

Adding Integers

We can do the same thing in binary if we can only remember…

\[\begin{align*} 0_2 + 0_2 &= 0_{10} = 00_2 \\ 0_2 + 1_2 &= 1_{10} = 01_2 \\ 1_2 + 1_2 &= 2_{10} = 10_2 \\ 1_2 + 1_2 + 1_2 &= 3_{10} = 11_2 \,. \end{align*}\]

(The 1+1+1 case happens when we add 1+1 and a carry.)

Adding Integers

When we add the bits in a column and get a sum that's two bits long (\(10_2\) or \(11_2\)), carry the one. Just like in decimal.

Adding Integers

Let's add these two:

\(10100110_{2} = 166_{10}\)
\(00110111_{2} = 55_{10}\)

Is the result \(221_{10}\)?.

Signed Integers

That's great, but we need to work with more than positive integers: we at least need negative values.

We'll represent signed integers with two's complement. Positive numbers will be the same as unsigned (with a lower upper-limit).

Signed Integers

The two's complement operation is used to negate a number.

Start with the positive number represented in binary;
flip all the bits (0↔1);
add one (ignoring overflow).

Signed Integers

So if we want to find the 8-bit two's complement representation of \(-21_{10}\)…

Start with the positive: 00010101
Flip the bits: 11101010;
Add one: 11101011.

So, \(-21_{10} = 11101011_2\).

Signed Integers

For a two's complement value, the first bit is often called the sign bit because it indicates the sign: 0=positive, 1=negative.

Signed Integers

It turns out the flip bits and add one operation doesn't just turn a positive to a negative. It negates integers in general. If we start with a negative…

\(11101011\)
flip the bits: \(00010100\)
add one: \(00010101_2 = 21_{10}\).

So, the two's complement value 11101011 was -21.

Signed Integers

It turns out the flip bits and add one operation doesn't just turn a positive to a negative. It negates integers in general. If we start with a negative…

\(11101011\)
flip the bits: \(00010100\)
add one: \(00010101_2 = 21_{10}\).

So, the two's complement value 11101011 was -21.

Signed Integers

It's not obvious why the flip bits and add one operation should be used to negate an integer: it's just the rule we're given and we'll have to trust that there's a reason. [There is.]

If it works, doing it twice should get you back where you started (because \(-(-x) = x\)). It's perhaps a surprise that the two's complement operation does that, but it does.

Signed Integers

Let's try some more 8-bit conversions…

11110011
00000110
10101000

Signed Integers

For a two's complement value, the largest positive value is 0111…111. For 8 bits, that's

\[\begin{align*} 01111111_2 &= 2^6 + 2^5 + \cdots + 2^1 + 2^0 \\ &= 64 + 32 + \cdots + 2 + 1 \\ &= 127_{10}\,. \end{align*}\]

Or in general, \(2^{n-1}-1\).

Signed Integers

The smallest negative value is 1000…000. To find the positive version, flip the bits and add one: 0111…111. Adding one to that causes a carry all the way to the first bit: 1000…000.

Signed Integers

The 8-bit version:

\(10000000\)
flip the bits: \(01111111\)
add one: \(10000000_2 = 128_{10}\).

So the two's complement value \(10000000_2\) represents \(-128_{10}\).

In general: \(-2^{n-1}\) up to the largest positive value, \(2^{n-1}-1\).

Signed Integers

The two's complement operation seems weird but it has one huge benefit: the addition operation is exactly the same.

It's perhaps surprising, but if we do the exact same addition operation (ignoring signs), then we get the correct result for two's complement values. We need one additional rule: if there's a carry out, a carry from the left-most position, throw it away.

Signed Integers

Let's consider the 4-bit example from earlier:

If throw away the carry-out, the result is 0101.

Signed Integers

If we do some conversions:

… we did correct two's complement addition before without realizing it.

Signed Integers

Let's try this example again, but think of them as two's complement:

\(10100110_{2} = -90_2\)
\(00110111_{2} = +55_2\)

Hopefully we got -35.

Signed Integers

Signed integer summary:

Starts with a 0: positive. Starts with a 1: negative.
To negate, do the two's complement operation: flip the bits and add one.
To add: like unsigned, but throw away carry-out.
If you're given bits, you can't tell if they're a signed or unsigned integer (or something else): you have to know (or the programming language has to).

Floating Point

We have seen that Python can handle floating point numbers and said they are close to (but not exactly) real numbers. (The same is true in other programming languages.)

We won't cover the details, but the idea is roughly binary values + scientific notation.

Floating Point

Instead of integer values, floating point values get represented as binary fractions with bits for \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{8}\), \(\frac{1}{16}\), \(\frac{1}{32}\), \(\frac{1}{64}\), \(\frac{1}{128}\), … .

Then multiply by a power of two.

So 40.5 would be represented as (some bits that mean): \[\left(\tfrac{1}{2} + \tfrac{1}{8} + \tfrac{1}{128}\right) \times 2^{6}\,.\]

Floating Point

Since we have to choose a fixed number of bits to do this, we can't represent every real number exactly.

In base 10, we can't represent \(\frac{1}{3}\) exactly (with a finite number of decimal digits): 0.333 is close but not exact.

Floating Point

The same thing happens in binary: there are often tiny errors in precision that can end up noticable.

>>> 0.3
0.3
>>> 0.1 + 0.2
0.30000000000000004

It seems like 0.1 + 0.2 should be exactly 0.3, but it's just a little different.

Floating Point

The same kind of thing is happening as trying to add \(\frac{1}{3}+\frac{1}{3}\) as 0.333 + 0.333 = 0.666 even though 0.667 is closer to \(\frac{2}{3}\).

For this course: don't panic. Just know that any floating point calculation can have tiny imprecisions. If you're doing serious numeric simulations or something, learn more.

Characters & Strings

We have also worked with strings (like "abc") which are made up of characters (like a).

Since we know how to represent (unsigned) integers already, characters are easy: just come up with a list of all characters and number each one. Then store the numbers.

Characters & Strings

The character ↔ number mapping is called a character set.

The most basic character set computers have used historically: ASCII (American Standard Code for Information Interchange). It defines 95 characters that can represent English text.

Characters & Strings

A few examples from ASCII:

Number	Character
32	space
37	%
82	R
114	r

The ASCII characters are basically the things you can type on a standard US English keyboard.

Characters & Strings

The 95 characters of ASCII aren't enough for French (ç) or Icelandic (ð) or Arabic (ج) or Japanese (の) or Chinese (是) or … .

Non-English speakers would probably like to use computers too (the computing industry realized eventually).

Characters & Strings

There's a historical story of character sets that I think is interesting, but I'll admit most people wouldn't. Eventually…

The Unicode character set was created to represent all written human language. It defines ∼150k characters currently and can be extended as needed.

Characters & Strings

Characters are organized into blocks by script/language/use.

Also included are various symbols and emoji: ↔, €, ≤, 𝄞, ♳, 😀, 🙈, 🐢, 💩.

Characters & Strings

Python strings are sequences of Unicode characters. (IDLE doesn't seem to handle Unicode characters perfectly in the editor, but the language handles them fine.)

>>> s = " %Rrðجの是↔€≤𝄞♳😀🙈🐢💩"
>>> print(s)
 %Rrðجの是↔€≤𝄞♳😀🙈🐢💩
>>> len(s)
17

Characters & Strings

If they're not on your keyboard, you can get characters into Python by copying-and-pasting or with a Unicode characters reference. I looked up C and found out it's hexadecimal (base 16) representation is 0043, so

>>> "\U00000043"
'C'
>>> "ab\U00000043de"
'abCde'

Characters & Strings

Your computer probably can display characters for common languages, but may not have a font that can represent less common characters/scripts.

e.g. a Chinese character that was added to Unicode recently (March 2020):

>>> "我吃\U00030edd\U00030edd面。"
'我吃𰻝𰻝面。'

Does it appear in that copy-pasted text for you?

Characters & Strings

On one computer, it appears just fine for me in IDLE:

On another it doesn't:

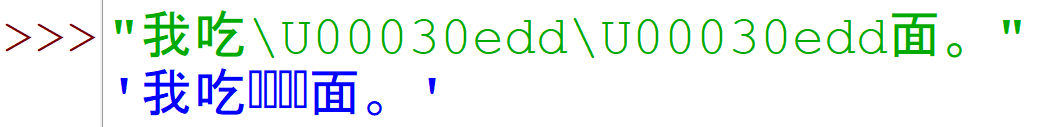
Characters & Strings

There are several ways to translate Unicode characters to/from bytes: character encodings. The details can wait for another course, but there's one almost-always-correct choice: UTF-8.

Depending on your text editor, there may be an option to select the character encoding or encoding when saving a file: choose UTF-8.

Characters & Strings

A text editor is program that lets you type some characters and saves the corresponding bytes to disk. We're using IDLE as a text editor (and also to run our Python code). There are many others (like Notepad++, Sublime Text, Brackets).

IDEs (Integrated Development Environments) like IDLE and Visual Studio combine text editing with help on the language or running the code.

Characters & Strings

Representing ASCII characters in UTF-8 takes one byte each. e.g. a space is character 32 and represented by the byte \[00100000_2 = 32_{10}\,.\]

If you open a text editor, type a single space, and save as UTF-8 text, the result should be a one-byte file containing that byte. (Maybe two bytes: some editors automatically insert a line break character.)

Characters & Strings

The file extension on a text file (.py, .txt) is just a hint about what kind of text the file contains. It's just bytes representing characters either way.

Compare something like a Word file (.docx) that contains information about formatting, embedded images, edit history, … .