Binary Representations
Binary Representations
Two things we know:
- Computers can store/manipulate only bits.
- We need computers to work with lots of other kinds of information: numbers, characters, dates, images, PDF documents ….
Counting
Let's teach you how to count. (This may be review.)
At some point, somebody taught you about positional numbers:
\[\begin{align*} 345 &= (3\times 100) + (4\times 10) + 5 \\ &= (3\times 10^2) + (4\times 10^1) + (5\times 10^0)\,. \end{align*}\]
Counting
We count in decimal or base 10: there are ten values (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) that can go in each position. Moving left a position increases the value by a factor of 10.
e.g. if we add a zero to the right of 345 to get 3450, the value is ten times larger.
Counting
But computers don't deal with ten distinct values. They have two: the bits, 0 and 1. Recall the reality of circuits:

So, computers count in binary or base 2.
Binary Integers
We do all the same positional number stuff, but with two instead of ten:
\[\begin{align*} 1001_2 &= (1\times 2^3) + (0\times 2^2) + (0\times 2^1) + (1\times 2^0) \\ &= 8 + 1 \\ &= 9_{10}\,. \end{align*}\]
Binary Integers
Unless it's completely clear, we should label values with their base as a subscript so they aren't ambiguous.
\[\begin{align*} 1001_2 &= (1\times 2^3) + (0\times 2^2) + (0\times 2^1) + (1\times 2^0) \,, \\ 1001_{10} &= (1\times 10^3) + (0\times 10^2) + (0\times 10^1) + (1\times 10^0) \,. \end{align*}\]
e.g. on the left, 1001
could be any base. On the right, math is pretty much always in base 10.
Binary Integers
In the same way that \(99999_{10} = 10^{5}-1\) is the largest five-digit base 10 number, \(11111_2\) is the largest five-bit base 2 number.
\[\begin{align*} 11111_2 &= (1\times 2^4) +(1\times 2^3) + (1\times 2^2) \\ &\qquad + (1\times 2^1) + (1\times 2^0) \\ &= 2^4 + 2^3 + 2^2 + 2^1 + 2^0 \\ &= 31 = 2^{5} - 1\,. \end{align*}\]
Binary Integers
… and zero is the smallest. This gives us enough to represent integers from \(0\) to \(2^{n}-1\) with \(n\) bits.
That's exactly how unsigned integers are represented when you use them in your code.
e.g. the uint16_t type from stdint.h represents integers exactly like this using 16 bits, so values 0 to \(2^{16}-1\) = 65535.
Binary Integers
Just like in decimal, leading zeroes don't change anything. e.g. we might write 1101 as 00001101 if we want to be clear that we're talking about an 8-bit value.
\[\begin{align*} 3456_{10} &= 000000003456_{10} \\ 1101_2 &= 00001101_2 \end{align*}\]
Binary Integers
We can get pretty far with just unsigned integers. Many different types of data can be represented with the right collection of unsigned integers.
For example, characters: if we make a list of all of the characters we need (e.g. A
, a
, θ
, अ
, 善
, 💩
) and assign each character a number, then we can represent text. (But Unicode is more complex. More later.)
Binary Integers
Another example, RGB colours are just brightnesses of the three primary colours (for the additive colour model): red, green, and blue.
We need to decide on a scale for the three components. Often (e.g. 24-bit colour depth RGB images) each component is an 8-bit integer: values 0–255 with 0 being dark
and 255 being bright
.
Binary Integers
Or in C syntax, a 24-bit RGB colour is:
struct rgb {
uint8_t red;
uint8_t green;
uint8_t blue;
};
Binary Arithmetic
We need to do more than just store numbers: we need to do calculations with them. Let's assume you know how to do that in decimal too.

In particular, when we add the values in a column and get a two-digit result, carry the one.
Binary Arithmetic
We can do the same thing in binary if we can only remember…
\[\begin{align*} 0_2 + 0_2 &= 0_{10} = 00_2 \\ 0_2 + 1_2 &= 1_{10} = 01_2 \\ 1_2 + 1_2 &= 2_{10} = 10_2 \\ 1_2 + 1_2 + 1_2 &= 3_{10} = 11_2 \,. \end{align*}\]
The 1+1+1 case happens when we add 1+1 and a carry. Remember the full adder circuit from our simple CPU example? It does exactly this.
Binary Arithmetic
When we add the bits in a column and get a sum that's two bits long (\(10_2\) or \(11_2\)), carry the one. Just like in decimal.

Binary Arithmetic
Did that work?
\[\begin{align*} 1110_2 &= 2^3 + 2^2 + 2^1 = 14_{10} \\ 0111_2 &= 2^2 + 2^1 + 2^0 = 7_{10} \\ 10101_2 &= 2^4 + 2^2 + 2^0 = 21_{10} \\ \end{align*}\]
Yup.
Binary Arithmetic
This last carry (the carry-out
) is exactly what the CF status flag is holding (or would be if we had 4-bit registers: same idea, just farther left).
The algorithms you learned to subtract, multiply, divide in decimal also work on binary.
But let's expand the kinds of values we can represent…
Signed Integers
We need to know how to represent negative integers: so far, we can do 14 but not -14.
I like negative numbers (and types like int32_t exist, so it's obviously possible.).
Signed Integers
One obvious-sounding solution (that turns out to kind of suck): just use one bit for the sign.
We could just use the first bit for 0=positive, 1=negative. That would let us represent negative integers.
Two problems: we have two zeros, -0 and +0. I don't think those are different integers. Also, addition gets weird. We can do better.
Two's Complement
We'll represent signed integers with two's complement. Positive numbers: anything starting with a 0 bit is positive and is then the same as unsigned (with a lower upper-limit). Anything starting with a 1 is negative.
The two's complement operation is used to negate a number.
- Start with the binary representation (of the positive value);
- flip all the bits (0↔1);
- add one (ignoring overflow).
Two's Complement
So if we want to find the 8-bit two's complement representation of \(-21_{10}\)…
- Start with the positive: 00010101
- Flip the bits: 11101010;
- Add one: 11101011.
So, \(-21_{10} = 11101011_2\) as an 8-bit two's complement value.
Two's Complement
Some things to note about that…
We had to decide how many bits we're using. With 8 bits, -21 became 11101011. With 16 bits, we'd get 1111111111101011.
The binary 11101011 is -21 if it's a signed integer, but 235 if it's an unsigned integer. We only know which is right
if we know which type we're trying to represent.
Two's Complement
It's easy to decide if a value is positive or negative: positive values start with a 0; negative values start with a 1.
The first bit is often called the sign bit because it indicates the sign: 0=positive, 1=negative.
Two's Complement
Why? We started with the premise that positive numbers are the same in signed and unsigned binary. Those all start with 0 (as long as we have enough
bits in the representation).
Doing the flip bits and add one
operation will change the first bit from 0 to 1 or 1 to 0 (again, if we have enough
bits: more later).
Two's Complement
It turns out the flip bits and add one
operation doesn't just turn a positive to a negative. It negates integers in general. If we start with a negative…
- \(11101011\)
- flip the bits: \(00010100\)
- add one: \(00010101_2 = 21_{10}\).
So, the two's complement value 11101011 was -21.
Two's Complement
To get the same number but with more bits, simply repeat the sign bit: the operation is called sign extending.
\[\begin{align*} 00010101_2 &= 0000000000010101_2 \\ 11101011_2 &= 1111111111101011_2 \end{align*}\]
The second equivalence is true for two's complement values, but not for unsigned values: we'd better know which we're working with.
Two's Complement
For signed integers, this is true. We must sign extend (repeat the sign bit) to make a longer version of the value. \[\begin{align*} 11101011_2 &= 1111111111101011_2 \end{align*}\]
For unsigned, we pad with zeros to make a longer representation of the same value: \[\begin{align*} 11101011_2 &= 0000000011101011_2 \end{align*}\]
Two's Complement
There are distinct x86 instructions for either operation, if we need to move a value from a smaller register to a larger one
The movsx instruction (Move With Sign-Extension) repeats the sign bit and movzx (Move With Zero-Extend) pads with zeros.
movsx %si, %rdi movzx %si, %rdi
Adding Two's Complement
It turns out two's complement has a lot of really nice properties: positive numbers are the same as unsigned; the sign bit there and easy to interpret; addition is surprisingly easy…
Adding Two's Complement
Addition is (almost) the same for both signed and unsigned binary integers. Let's look at this again:

Adding Two's Complement

The problem is the leftmost 1 bit which that makes the binary value longer (4 to 5 bits).
That's called the carry bit: the possible carry past of the number of bits we started with.
Adding Two's Complement

For two's complement addition, we'll discard the last carry, so the result here would be 0101.
Adding Two's Complement
If we do some two's complement conversions…
\[\begin{align*} 1110_2 &= -(0001_2 + 1) = -2_{10} \\ 0111_2 &= 2^2 + 2^1 + 2^0 = +7_{10} \\ 0101_2 &= 2^2 + 2^0 = +5_{10} \\ \end{align*}\]
… we got \(-2 + 7 = 5\).
Adding Two's Complement
This is true in general: as long as we're not close to the limits (biggest/smallest values: more later), signed and unsigned addition are the same thing.
That simplifies things for the processor: all integer additions are the same. That's why we have only add for integer addition: it handles both.
Adding Two's Complement
But what if we are close to the limits? Let's do some
Adding Two's Complement
The largest positive integer is \(0111_2 =7_{10} \). If we add one to it:

Adding Two's Complement
The result was \(1000_2\). If we negate:
- \(1000\)
- flip the bits: \(0111\)
- add one: \(0111 + 1 = 1000_2 = 8_{10}\).
So the result was -8? That's the smallest negative value.
Aside: if we look at those as unsigned integers, the result was correct: 8.
Adding Two's Complement
There was a signed overflow: we exceeded the range of values that could be represented in a 4-bit signed integer, so the addition algorithm gave an incorrect
result.
How can we detect that in the operation?
Adding Two's Complement
We need to look at the sign bits:

There is a signed overflow if: the input sign bits are the same, and the output sign bit is different than them.
Adding Two's Complement
If we call \(s_X\) the sign bit of \(X\) and we're doing \(A+B=C\), that would be:
\[ (s_A = s_B) \wedge (s_A \ne s_C) \]
There can be no overflow if \(s_A \ne s_B\): adding a positive and a negative can never overflow.
Adding Two's Complement
The signed overflow just described is exactly the x86 OF flag: we can check it to see if a signed operation overflowed. (e.g. with the jo and jno instructions.)
The carry flag is the x86 CF flag: it will tell us if an unsigned operation overflowed. (e.g. with the jc and jnc instructions.)
Other Operations
Most of that story is the same for subtraction (because we know that \(A-B = A + (-B)\) and we know negation is easy).
There's also only a single integer subtraction instruction: sub.
It sets CF for unsigned overflow and OF for signed overflow.
Other Operations
The story is a little more complex for multiplication and division. The way the operation is done, and the way overflow is detected are different.
There are separate mul and div instructions for unsigned integers, and imul and idiv for signed integers.
Other Operations
While we're on the subject… the integer multiplication and division instructions on x86 are weird.
Other Operations
The mul instruction (unsigned) takes a single operand that must be a register, and multiplies %rax by that value, putting the result in %rdx:%rax (i.e. it's a 128-bit result with the high bits in %rdx and low in %rax).
Other Operations
The imul instruction (signed) can do that if given one operand, or if given two it works like other instructions:
does a imul a, b
operation with the limitation that b*=ab must be a register (not a memory reference).
mul and imul set OF and CF like you'd probably expect: if the product doesn't fit in one register (64-bits), it's considered an overflow.
Other Operations
Similar story for division: div takes one operand and divides %rdx:%rax by it. So if you want to divide, you have to set both %rdx and %rax. Probably %rdx to zero and %rax to the numerator.
For signed division, the idiv instruction is similar to div: one operand, dividing %rdx:%rax by the given value.
Other Operations
Both of the integer division operations put the remainder in %rdx (and quotient in %rax).
An implication: in C, if you're already doing a/b, doing a%b fairly close-by should be free: the compiler should be smart enough to capture both after the single div/idiv instruction. [later topic: “compiler optimization”]
Limits and Overflow
As mentioned before, the smallest and largest values for \(n\)-bit unsigned integers are:
\[\begin{align*} 000\ldots{}000_2 &= 0 \\ 111\ldots{}111_2 &= 2^n - 1 \end{align*}\]
So, the max is 255 for 8 bits, 65535 for 16-bits (and numbers I don't remember for 32- and 64-bit values).
Limits and Overflow
For \(n\)-bit signed integers, the most-negative value is:
\[ 1000\ldots{}000_2 = -2^{n-1} \]
And the largest positive number is:
\[ 0111\ldots{}111_2 = 2^{n-1} - 1 \]
For 8 bits, that's -128–127.
Limits and Overflow
When we're doing arithmetic on these values in assembly, we expect it to do the calculation as requested. The general rule if values don't fit in the number of bits we're using: keep only the bits that will fit.
The carry flag and overflow flag tell us when we have exceeded those limits.
Limits and Overflow
e.g. for a signed 8-bit addition, we would expect \(+127 + 1\) to be:

… -128, with OF set.
Limits and Overflow
e.g. for an unsigned 8-bit addition, we would expect \(255 + 1\) to be:

… 0, with CF set.
Limits and Overflow
As with everything else in assembly, there are no safeguards: the circuit does the calculation we ask for and it's up to us to interpret the results.
The net effect: we get a kind of wraparound
behaviour on these operations.
Solution 1: check the overflow/carry flags after every operation. Solution 2: make sure you use enough bits for the values you're working with so there is no overflow/carry.
Limits and Overflow
For unsigned operations, the carry flag (CF) generally indicates an overflow. We can check it with jc or jnc.
Let's write a function that adds one to an unsigned 8-bit value and checks for carry…
Limits and Overflow
Let's try it. We'll use the 8-bit registers so it's easier to see what's happening. For unsigned integers, we expect this to overflow if the function argument is 255. (%dil is the low 8 bits of %rdi.)
overflow_unsigned:
add $1, %dil
jnc ou_no_carry
call print_uint64
If it does carry, we expect the result of the 8-bit addition, truncated to fit in 8 bits: 0.
Limits and Overflow
For a signed integer, we expect this to overflow if the argument is 127.
overflow_signed:
add $1, %dil
jno os_no_overflow
movsx %dil, %rdi # convert to 64-bit value
call print_int64
Note: previous example was jnc (or jc for the opposite jump) on the CF bit. This is jno (or jo) on the OF bit.
This will print -128 when it overflows.
Limits and Overflow
overflow_signed:
add $1, %dil
jno os_no_overflow
movsx %dil, %rdi # convert to 64-bit value
call print_int64
Note also: the movsx instruction to sign-extend the value to 64-bits for the print_int64 function: it needs a 64-bit signed integer argument and we have 8-bit signed.
Why didn't we need anything analogous for the previous (unsigned) example?
Languages & Limits
Don't confuse what happens in assembly with what happens in your favourite programming language: a language is free to define (and enforce) its own behaviour on its types. The language's compiler and/or runtime environment will give you the behaviour they promise.
I was surprised how different common languages are…
Languages & Limits
In Go, the language promises two's complement arithmetic behaviour for signed integers, and that's what you get.
var n int8 = 127 n = n + int8(1) fmt.Println(n)
That prints -128: we get the same wraparound behaviour we expect from assembly.
Languages & Limits
Python does normal 64-bit signed arithmetic when it can, but if values pass the limits of that type, it switches to a large integer representation and carries on. (i.e. maybe something like GNU GMP that can represent and do arithmetic on arbitrarily-large integers.)
Calculations are going to be slower out of the 64-bit signed range, but the programmer doesn't have to worry about overflow.
Languages & Limits
e.g. this Python code: (** is the power operator in Python)
# calculate 2**63 - 1 without overflowing n = (2**62 - 1) * 2 + 1 print(n) print(n + 1) # *now* overflow print(n**2) # go far past 2**64 print(factorial(45)) # even farther
… prints:
9223372036854775807 9223372036854775808 85070591730234615847396907784232501249 119622220865480194561963161495657715064383733760000000000
Languages & Limits
Rust is delightfully pedantic. The normal integer types (e.g. i8 for 8-bit signed integers) detect overflow and panic (≈ throw an exception) when compiled debug mode but not in release mode.
If we set n to 127, this code panics with an error attempt to add with overflow
:
let a: i8 = n;
let b: i8 = 1;
println!("{:?}", a + b);
Languages & Limits
But there's a different Rust type Wrapping that can turn an integer type into one that does two's complement behaviour (or the wraparound behaviour we expect in assembly for unsigned).
This code will print -128 with n==127:
let a: Wrapping<i8> = Wrapping(n);
let b: Wrapping<i8> = Wrapping(1);
println!("{:?}", a + b);
Languages & Limits
Or there's a Saturating type (since Rust 1.74, unstable before that) where if you try to calculate a value past the limits, it just stops at the smallest/largest value.
This code will print 127 with n==127:
let a: Saturating<i8> = Saturating(n);
let b: Saturating<i8> = Saturating(1);
println!("{:?}", a + b);
i.e. when we tried to add one to 127, the result would be out-of-bounds, so it returns the largest possible value of that type, 127.
Languages & Limits
Or you can explicitly say check for overflow, even in release compilations
. Then you get a checked result (a Rust Option) that you must examine.
let a: i8 = n;
let b: i8 = 1;
match a.checked_add(b) {
Some(s) => println!("{:?}", s),
None => println!("Overflow!"),
};
Languages & Limits
Or we can just ask for the unchecked addition and the carry bit (as a bool)
let a: i8 = n;
let b: i8 = 1;
let (sum, carry_out) = a.carrying_add(b, false);
println!("{:?} {:?}", sum, carry_out);
Languages & Limits
C is weird.
In C (and C++), there are a lot of things the programmer might do where the result is undefined. That is, the language makes no promise about what the result might be.
Languages & Limits
The program might calculate a result you expected; it might throw an exception; it might calculate something you think is incorrect
.
All of those are correct results for a C compiler to produce when faced with undefined behaviour. Different compilers might do different things, changing optimization level might change the output, etc.
Languages & Limits
Integer overflow is one of those. In C, there is no correct result to exceeding integer limits. The compiler is free to do whatever it likes.
int8_t n = 127;
printf("n == %hhi\n", n);
int8_t n1 = n + 1;
printf("n + 1 == %hhi\n", n1);
For me, today, on a specific compiler, that code prints:
n == 127 n + 1 == -128
Any correct C compiler must print 127 on the first line. The second printf could give literally any result.
Languages & Limits
For me, this code prints
for the argument falseINT64_MAX with compiler optimization off, but
with any optimization turned on with Clang (but always true
with GCC).false
void is_max(int64_t n) {
if ( n + 1 > n ) {
printf("true\n");
} else {
printf("false\n");
}
}
Languages & Limits
void is_max(int64_t n) {
if ( n + 1 > n ) {
printf("true\n");
} else {
printf("false\n");
}
}
The compiler analysis of this function sees two cases: (1) there is no overflow, so the condition is true, (2) there is an overflow, then it doesn't matter what happens. So, it throws away the false case because it's unreachable by any well-defined operation.
Languages & Limits
With compiler optimization, that function compiles to the exact same assembly code as this:
void is_max(int64_t n) {
printf("true\n");
}
Any of that story might change for a different compiler or version or optimization level. All of them are correct compilations.
Languages & Limits
There is lots of C code that will do something, but it might change at any moment because it's undefined in the language spec. Asking the programmer to keep track of which things in the language have undefined behaviour is (in my mind), unreasonable.
But that's C.
Languages & Limits
All of those are reasonable designs for a programming language (except arguably C).
As a programmer, knowing what the machine instruction will do can illuminate how a programming language works, but it might not be the whole story.
Hexadecimal
Back to representing integers…
We usually represent integers in decimal: base 10. We have also seen binary: base 2.
It turns out hexadecimal or base 16 (or hex) is also often useful.
Hexadecimal
We need more digits (hexits
?) if we're going to have 16 possible values in each position. We'll head down the alphabet. The 16 hexadecimal digits:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
From 0 to 9, same as you'd expect: \(9_{16} = 9_{10}\).
From there, we keep counting: \(\mathrm{A}_{16} = 10_{10}\)… \(\mathrm{F}_{16} = 15_{10}\).
Hexadecimal
Base 16 is convenient because you can represent exactly 4 bits with one hex-digit:
\[ 0000_2 = 0_{10} = 0_{16} \,, \\ 1001_2 = 9_{10} = 9_{16} \,, \\ 1100_2 = 12_{10} = \mathrm{C}_{16} \,, \\ 1111_2 = 15_{10} = \mathrm{F}_{16} \,. \]
Hexadecimal
So, hexadecimal values are still nicely related to binary, but it's much easier to look at. \[\begin{align*} &\quad 12345678_{10} \\ &= 1011\,1100\,0110\,0001\,0100\,1110_{2} \\ &= \mathrm{BC614E}_{16} \end{align*}\]
e.g. the least significant 4 bits are 1110 which map exactly to the last E in the hex representation.
Hexadecimal
In code (in many languages), you can give values in base 10 (as you're probably used to) but also express values in hexadecimal with a 0x prefix or in binary prefixed with 0b.
These initialize C variables to the same value:
uint64_t a = 28; uint64_t b = 0x1c; uint64_t c = 0b11100;
Hexadecimal
Or similarly in Python:
a = 28 b = 0x1c c = 0b11100
Or these are equivalent assembly:
mov $28, %rax mov $0x1c, %rbx mov $0b11100, %rcx
Hexadecimal
Hexadecimal is useful when you're thinking about binary, but don't want to look at 64 characters to represent a 64-bit value. Compare the largest unsigned 16-bit value:
65535
0xffff
0b1111111111111111
I think the hex representation is much more obvious.
Hexadecimal
Hex can definitely be more clear when looking a value where the bits matter more than the overall values. Compare these equivalent instructions:
and $8192, %rax and 0x2000, %rax and 0b10000000000000, %rax
It was \(2^{13}\): only bit 13 was set.
Other Data in Binary
That gives us one thing we can represent in binary: integers. (Maybe two, if you count signed integers as a separate thing.)
But that can get you pretty far, as in the RGB colour example: if you can store it with multiple integers, figure out how many integers you need, and what kind of range they need to have. Consider them a struct or class or similar in some programming language.
struct rgb {
uint8_t red;
uint8_t green;
uint8_t blue;
};
Other Data in Binary
For example, maybe we want to store a date: year, month, day. We could do something like this:
struct date {
int16_t year;
uint8_t month;
uint8_t day;
}
That would let us represent years -32768–+32767 and months 1–12 and days 1–31. There is a little extra capacity, but that might not be so bad.
Other Data in Binary
Or, we could represent the day as a single integer: the number of days after some start of time
day (the epoch). So, we could just store a single int32_t and say today is 10000 days after the start of time, tomorrow is 10001. It would certainly make date arithmetic easier.
Neither of those representations of a date is crazy: choosing might depend on how it's being used.
Other Data in Binary
If we also wanted dates with times (often called a datetime
or timestamp
), we could represent a date and time as seconds after the start of time
.
That's exactly how Unix timestamps work. The conventional way to represent a timestamp (e.g. last modified time on a file) is a number of seconds after January 1, 1970 at 00:00 UTC.
Other Data in Binary
e.g. in Python, the time.time function returns the number of seconds since the Unix epoch:
>>> import time >>> time.time() 1764006744.1543596
… and that's a fairly widely-understood way to express that idea (but it does not express the timezone, which isn't great).
As you can see here: it's also possible to have sub-second precision by using a floating point value instead of an integer.
Other Data in Binary
There are also some values that are better expressed with floating point values. [later topic: “floating point”]
Characters
Characters are an important type of data we need to store, with a bunch of historical baggage. Early computers all did their own (incompatible) things.
The first common standard for representing characters was ASCII: American Standard Code for Information Interchange. As you might guess from the name, it is designed for English only.
Characters
ASCII defines 127 characters: basically the ones on a standard US keyboard: space, basic punctuation, digits 0–9, letters A–Z and a–z.
Characters
ASCII includes 32 control characters. e.g. null ('\0'), tab ('\t'), newline ('\n'), bell ('\a').
The control
characters correspond to the control key on your keyboard: character 1 maps to a ctrl-A keypress in command-line/text systems; ctrl-B produces character 2, etc.
Characters
In some ways, the control characters feel like historical curiosities (e.g. character 4 is end of transmission
; 11 is device control 1
), but some still leak into our world.
Character 0 is null
or '\0' and marks the end of a C string in memory.
Character 4 is end of transmission
and corresponds to ctrl-D. Pressing ctrl-D will exit most command-line tools (in Unix/Linux).
Characters
The various whitespace characters are control characters: character 9 is tab '\t'; 10 is newline '\n'; 13 is '\r' carriage return.
The bell (character 7, '\a') might still work.
print('\a')
echo -e \\a
Characters
With only 127 characters, it's easy to represent ASCII characters in 7 bits. Most computers would use a single byte for each ASCII character.
Great, except languages besides English exist.
Characters
There were several extensions to ASCII to use the rest of a single byte: ISO-8859-1 for western European languages (ASCII + characters like é, ñ, £); ISO-8859-7 for Greek characters (ASCII + α, β, γ, …).
But with only one byte per character, only one of the extensions could be used at a time: no mixing French and Greek.
Characters
Each of these is a character set: a collection of characters it's possible to represent, and give each one a number so it can be represented with an integer.
e.g. in ASCII (and all extensions of ASCII), we want to represent the character A
and it's character number 65. The lower case a
is character 97.
Characters
As long as we have ≤256 characters, we can represent that integer with one byte as an unsigned integer. Easy.
This is the world the C char data type imagines. It's defined as a single byte, so it can hold a character
, as long as we don't acknowledge the existence of people outside of Europe, and don't imagine anyone in Europe would want to communicate across languages.
Characters
There are plenty of languages that use >256 characters. As a result, there are several multi-byte character sets. e.g. Shift JIS for Japanese, GB 18030 for Chinese, Big5 also for Chinese use 1–4 bytes per character.
These also can't be mixed: each defines what each combination of bits does, so you have to choose only one in a file/string/whatever.
Characters
So, Unicode was created. Simple goal: represent every possible form of written communication in one character set. Easy. /s
If we have one character set that can represent any written text, we can mix languages in a single string/document.
Characters
Step 1: make a list of every character humans use to express themselves. (How hard could it be? Currently around 160,000 are defined.)
Step 2: give each one a number. (Easy, once you have the list.)
Step 3: represent those with bits. (Hmmm…)
Characters
With >100k characters, the obvious big enough unsigned integer
strategy starts to seem questionable. I don't want to use 3+ bytes for every character I need in a string/file.
And coming from an Anglo-centric perspective (as many making the decisions were), that seems a lot worse than the one-byte character sets that preceeded it.
Characters
The choice isn't obvious. The Unicode character set has several encodings or character encodings: ways to turn the character numbers into bits.
We could do the obvious thing: the UTF-32 encoding just uses 32 bits (4 bytes) for each character. That means simple encoding, but it's a lot of bytes per character.
Characters
The UTF-16 encoding uses 16 bits for many characters. The first 216=65536 character numbers can be represented with two bytes. Characters beyond that need 4 bytes (32 bits, a surrogate pair
).
The first 216 Unicode characters are known as the basic multilingual plane, BMP.
Characters
The problem: it's very easy to look at UTF-16-encoded text and incorrectly think character = 2 bytes
. Many programmers have. Then users do perfectly reasonable things (like use an emoji) and everything breaks.
My advice: avoid UTF-16. It's too easy to get wrong.
Characters
If you have seen a system (web site or something) where it seems like Unicode works, but you can't use emoji, treating UTF-16 as if it's two bytes per character is a possible cause.
UTF-8
We have a much more clever option: UTF-8 where characters take up to four bytes.
UTF-8 uses a very clever number ↔ bytes method that leaves many characters taking <4 bytes, but can still represent all of Unicode. It encodes different characters with a different number of bytes.
UTF-8
We can break the character numbers up by the number of bits needed to represent them as an unsigned integer (left-padding with 0s as needed). Each character takes 1–4 bytes:
| n bits | Byte 1 | Byte 2 | Byte 3 | Byte 4 |
|---|---|---|---|---|
| n≤7 | 0xxxxxxx | |||
| 7<n≤11 | 110xxxxx | 10xxxxxx | ||
| 11<n≤16 | 1110xxxx | 10xxxxxx | 10xxxxxx | |
| 16<n≤21 | 11110xxx | 10xxxxxx | 10xxxxxx | 10xxxxxx |
UTF-8
To encode a character as UTF-8:
- Look at how many bits are needed to represent the character number as an unsigned binary integer.
- Find the right row of the table.
- Replace the
x
in the table with the bits of the unsigned integer (left padding with 0s as needed).
Those are the bytes representing that character as UTF-8.
UTF-8
When you see a byte from UTF-8 encoded text, you know immediately what kind of character you're looking at.
e.g. any byte with first bit 0 must be a one byte character (first row of that table).
e.g. 11001111 starts with 110
: it can only be the first byte of a two-byte character. The next byte must start with 10
. Then we take the other bits (in the x
positions in the previous table) and decode that binary.
UTF-8
e.g. if we see 11001111 (marking the bits that I can see in the table, not as x
), followed by 10000110 we have encoded the bits 01111 (from the first byte) and 000110 (from the second byte).
Together, that's 011110001102 or 96610 as an unsigned integer. Character number 966 is φ
: greek lowercase phi.
UTF-8
Suppose we see these bytes as UTF-8 input. (Again, bits I can see specified in the UTF-8 encoding table highlighted; the others are the data
.)
11110000 10011111 10011000 10101000 00111111
It must be a 4-byte character followed by a 1-byte character. The data
bits (with spaces to separate the contribution from each byte):
000 011111 011000 101000
0111111
UTF-8
000 011111 011000 101000
0111111
That's integers 12855210 and 6310. In the table of Unicode characters, I find Fearful Face Unicode Character
and question mark
.
>>> data = b'\xf0\x9f\x98\xa8\x3f'
>>> s = data.decode('utf-8')
>>> s
'😨?'
>>> [f'{b:>08b}' for b in data]
['11110000', '10011111', '10011000', '10101000', '00111111']
>>> [f'{b:>08b}' for b in s.encode('utf-8')]
['11110000', '10011111', '10011000', '10101000', '00111111']
UTF-8
In the other direction, suppose we want to UTF-8 encode the character 是. That's Unicode character 2615910 or 1100110001011112.
The integer needs 15 bits, so we look to row 3 of the table. Left-pad to 16 bits to get:
0110011000101111
UTF-8
Break into chunks as large as the x
fields in that row of the table:
0110 011000 101111
And put them into those places in the binary in that row to get the bytes:
11100110 10011000 10101111
= E6 98 AF16
>>> b'\xE6\x98\xAF'.decode('utf-8')
'是'
UTF-8
There's still a little Eurocentrism in the encoding: English characters take one byte; most European languages are in the two-byte range of characters; you need three bytes per character to get to Asia.
But the single-script Chinese and Japanese character sets are also 1–4 bytes per character, so maybe it's not so bad?
UTF-8
ASCII characters (0–127) are represented with one byte in UTF-8. That's good: it means all ASCII text is also UTF-8 text, but it leaves the same danger of programmers testing with only ASCII characters and assuming character = 1 byte
.
UTF-8
The C single-byte
type doesn't help programers get things right. Remember that chararray of bytes
≠ array of characters
. Array of bytes = collection of encoded characters that need to be decoded before they can be treated as text.
UTF-8
If you're dealing with text in your code, don't be that programmer.
Always test your code with non-ASCII, and probably with characters that take 4 bytes in UTF-8. Many (but not all) emoji are in that range.
The one I can always remember: 💩. As UTF-8, it's four bytes:
11110000 10011111 10010010 10101001
UTF-8
Remember that in a lot of content, there's a lot of ASCII even when the natural language isn't English. e.g. some HTML:
<title>你好</title>
That's 17 characters and takes 21 bytes to encode in UTF-8.
UTF-8
In Python:
>>> s = '<title>你好</title>'
>>> len(s)
17
>>> len(s.encode('utf-8'))
21
>>> [int(byte) for byte in s.encode('utf-8')]
[60, 116, 105, 116, 108, 101, 62, 228, 189, 160, 229, 165,
189, 60, 47, 116, 105, 116, 108, 101, 62]
Text
If you're working with text in a user-facing way (e.g. the user can type stuff and you have to store it), Unicode support should be considered non-negotiable. UTF-8 is probably the right choice of encoding, unless proven otherwise.
Text
If you're working with text coming from outside of your code (reading a file, network input, etc), you must know the character set and encoding to know how to handle it. If you don't, you can't correctly process it.
There is often a default encoding your language/system will use, but there's no guarantee it's the right one.
Text
An example starting with UTF-8-encoded text:
>>> input_bytes = bytes([102, 111, 114, 195, 170, 116, 32,
100, 195, 169, 106, 195, 160, 32, 118, 117])
>>> input_bytes.decode('utf-8') # decode correctly as UTF-8
'forêt déjà vu'
>>> input_bytes.decode('iso-8859-1') # decode incorrectly
'forêt déjà vu'
>>> as_8859_1 = input_bytes.decode('utf-8').encode('iso-8859-1')
>>> [int(b) for b in as_8859_1] # correctly encoded ISO-8859-1
[102, 111, 114, 234, 116, 32, 100, 233, 106, 224, 32, 118, 117]
>>> as_8859_1.decode('iso-8859-1') # correctly decoded
'forêt déjà vu'
>>> as_8859_1.decode('iso-8859-7') # incorrectly decoded
'forκt dιjΰ vu'
>>> as_8859_1.decode('utf-8') # it's illegal UTF-8
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
UnicodeDecodeError: 'utf-8' codec cant decode byte 0xea in position 3: invalid continuation byte
Text
There's no such thing as plain text
. It doesn't exist. A text file
or plain text
or similar are all a lie.
There's only text stored with a specific character set/encoding. Take a moment and think about it when you have to read bytes, and choose appropriately.
Textbooks will usually do this wrong. In Java, the relevant argument (to FileReader) wasn't added as an option until Java 11 (2018!).
FileReader fr = new FileReader(file, StandardCharsets.UTF_8); BufferedReader br = new BufferedReader(fr);
Text
Text files (.txt, .c, .java, .py, .html, .svg, .json, …) are just the bytes representing each character in a file.
i.e. if you open a text editor, type a single space, and save as UTF-8 text, the result should be a one-byte file containing 0x20. (Maybe two bytes: some editors automatically append a line break.)
There's (in general) no metadata and no declaration of the character set/encoding: you have to know what you're reading and decode correctly.
Text
There might be some metadata or explicit encoding specified that will guide you to the correct way to read/write specific text files.
e.g. Rust source must be UTF-8 text, or an HTTP resource might have a charset (indicating both character set and encoding) specified in the response headers. (But do you know the encoding of HTTP headers?)
Content-Type: text/plain; charset=utf-8
Text
Some text-based formats have a declaration of character encoding that can be read as long as the actual encoding is a superset of ASCII. (i.e. start reading the file as ASCII text, find the declaration, then start over with the right encoding.)
<?xml version="1.0" encoding="utf-8"?>
<meta charset="utf-8" />
@charset "utf-8";
# -*- coding: <encoding utf-8> -*-
Strings
But what do programming languages do internally? That also depends.
In general, strings are just a sequence of characters, but the way languages handle both varies.
Strings
In Rust, strings (the str and String types) are explicitly UTF-8 encoded Unicode text in memory. This is perfectly legal Rust code (if saved in a UTF-8-encoded .rs file).
let message = "Hello 😃";
println!("{}", message);
Hello 😃
Strings
But then (in Rust and other languages), there's a question about that string's length
. It's 7 Unicode characters, but 10 bytes encoded in UTF-8 (6 ASCII characters + 4 bytes for the emoji).
Rust can tell you both, but you have to know how to ask (and I'm fairly sure .chars().count() is an \(O(n)\) operation).
println!("{}", message.len());
println!("{}", message.chars().count());
10 7
Strings
In Python 3, strings (the str type) are Unicode characters, encoded somehow in memory.
message = "Hello 😃" print(message) print(len(message))
Hello 😃 7
Strings
A separate type, bytes holds a byte string
: series of bytes representing arbitrary data. Strings are encoded to bytes with a specific character encoding.
encoded = message.encode('utf-8')
print(type(message))
print(type(encoded))
print(len(encoded))
print(encoded.decode('utf-8') == message)
<class 'str'> <class 'bytes'> 10 True
Strings
In C, it's all a mess.
The char type holds bytes, not characters. All of those char[] you have used have been byte arrays that you have implicitly assumed hold ASCII text.
The wchar_t type (wide character) is generally larger that char, but the language spec doesn't say how big, so it's not clear how cross-system compatible it will be.
Strings
The most-correct solution seems to be the C++ std::basic_string containing char32_t, which is a u32string.
typedef basic_string<char32_t> u32string;
Then you can put UTF-32-encoded text in that (but the language still doesn't specify that's what you must do: it could be any 32-bit character encoding in that type).
Strings
Basically: if I had a choice of languages to do text processing, it wouldn't be C or C++.
At least find some maximally-beautiful string library to make things easier for you.
Unicode is Complex
Also note that Unicode is probably more compilicated than you think.
s1 = 'é' s2 = 'é' print(s1, s2) print(len(s1), len(s2))
é é 1 2
Unicode is Complex
import unicodedata print([unicodedata.name(c) for c in s1]) print([unicodedata.name(c) for c in s2])
['LATIN SMALL LETTER E WITH ACUTE'] ['LATIN SMALL LETTER E', 'COMBINING ACUTE ACCENT']
One is a single e with an accent
character. The other is an ASCII e
followed by accent that combines with the previous character
. But they look the same: é é.
Unicode is Complex
Simply comparing Unicode text for equality (equivalence) or sort order (part of collation) is shockingly hard.
Unicode is Complex
The transformation between these representations of the same characters
is Unicode normalization.
>>> def char_nums(str):
... return [ord(c) for c in str]
>>> s1, s2 = 'é', 'é'
>>> char_nums(s1)
[233]
>>> char_nums(s2)
[101, 769]
>>> import unicodedata
>>> char_nums(unicodedata.normalize('NFC', s1))
[233]
>>> char_nums(unicodedata.normalize('NFD', s1))
[101, 769]
>>> char_nums(unicodedata.normalize('NFC', s2))
[233]
>>> char_nums(unicodedata.normalize('NFD', s2))
[101, 769]
Unicode is Complex
Even with normalizing, things are more complicated that I would have guessed.
>>> q1 = '¼'
>>> char_nums(q1)
[188]
>>> q2 = unicodedata.normalize('NFKC', q1)
>>> q2
'1⁄4'
>>> char_nums(q2)
[49, 8260, 52]
>>> [unicodedata.name(c) for c in q1]
['VULGAR FRACTION ONE QUARTER']
>>> [unicodedata.name(c) for c in q2]
['DIGIT ONE', 'FRACTION SLASH', 'DIGIT FOUR']
Unicode is Complex
Even the concept of character
isn't as clear as you might like.
This is 5 characters that encode as 19 bytes in UTF-8:
🫱🏼🫲🏾
Unicode is Complex
Don't believe me?
handshake = '🫱🏼🫲🏾'
print(handshake)
print(len(handshake))
print(len(handshake.encode('utf-8')))
🫱🏼🫲🏾 5 19
Unicode is Complex
The five characters are:
- Rightwards Hand 🫱
- Medium-light brown skin tone modifier 🏼
- Zero Width Joiner
- Leftwards Hand 🫲
- Medium dark skin tone modifier 🏾
Or, in short: 🫱🏼🫲🏾.
Unicode is Complex
Here's how that Python code looks in two different text editors, and the output in the terminal for me:
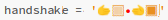


So how many characters
is it really? I don't know.