Bit Tricks
Bit Tricks
Now that we know a little more about how computers represent things (especially integers), there are a lot of ways we can use that to work with those values in our code.
Terminology aside: if a bit is holding a 1, it's common to say the bit is set and for 0 it's cleared.
Bit Tricks
We have already seen the sign flag, SF that we can use with the js and jns instructions.
But all the processor is doing: copy the highest bit from the calculation and call it SF. So, SF is useful and convenient, but we're just inspecting one bit from the result and using it to make a decision.
We can do the same thing with other bits, if that's useful.
Bit Tricks
For example, when we test for even/odd integers, this is the typical C code:
if ( n%2 == 0 ) {
printf("even");
} else {
printf("odd");
}
Bit Tricks
We could implement that directly in assembly: idiv, and look at the remainder.
That would mean using idiv (recall: it divides %rdx:%rax by its argument, which must be a register, and puts the remainder in %rdx). This will compute rdx = rdi%2:
mov $2, %r8
mov $0, %rdx
mov %rdi, %rax
idiv %r8
Bit Tricks
The problem: doing the division is very expensive: it takes 39–103 cycles to do a 64-bit idiv on Haswell [Agner Fog's Instruction tables, p. 248].
We can do much better. We really just need to know if the least-significant bit is set: odd numbers have a 1 in the least-significant bit; even numbers don't.
e.g. \(6_{10} = 00000110_2\) and \(-1_{10} = 11111111_2\).
Bit Tricks
The and instruction does bit-wise AND between its two operands: bit-by-bit, do an AND operation on each position, and that's the result.
The number 1 has only the least significant bit set, so if we AND it with anything, we're left with only the least-significant bit:
00101101 11101010
AND 00000001 AND 00000001
= 00000001 = 00000000If we do that and get zero, it was even.
Bit Tricks
We can use that to do the same thing: this code also does rdx = rdi%2:
mov %rdi, %rdx
and $1, %rdx
That does the same thing as the idiv solution and is about 10 times faster (with a quick test on one computer).
Bit Tricks
Using a bit-wise AND operation to examine certain bits is a bit mask. e.g. we can examine bits 2 and 3 (or whatever you call the \(2^2\) and \(2^3\) place) by ANDing with 0b1100 == 12:
00101101 11101010
AND 00001100 AND 00001100
= 00001100 = 00001000Bit Tricks
After n & 0b1100 we are left with only bits 2 and 3 of n (four possible values) and could check which we get:
int8_t bits23 = (n & 0b1100);
if (bits23 == 0b1100) {…}
else if (bits23 == 0b1000) {…}
else if (bits23 == 0b0100) {…}
else if (bits23 == 0b0000) {…}
Bit Tricks
The lesson: computers are good at manipulating bits. If you can phrase your operation directly as a bit manipulation, it will probably be fast.
Also, not all instructions are equal: the processor has a lot more work to do for idiv than and. They both look like one instruction in assembly code, but there's more to know about how the processor handles them.
Bit Tricks
Should we change our C code in this case?
No. No no no no. tl;dr no.
The compiler's optimizer is quite capable of transforming the idiom that everybody understands and can read at a glance (n%2==0) into fast assembly code (and possibly faster that what we would write by hand).
Write beautiful code and let the compiler do its job. [later topic: “compiler optimization”]
Bit Tricks
But there are some more things we can do in assembly, which might sometimes change the way we approach things in other languages. Abstractions leak.
Bit Fields
There are often cases where you have to store a lot of yes/no or on/off or similar Boolean values. e.g. you have millions of records, and each might be displayed
or not, each might be active
or not, or any other boolean properties you can imagine.
Several bits like that can be stored as a bit field that can represent many bits in a single integer.
Bit Fields
I'm going to switch to C.
The basic operations we need are bit-by-bit AND, OR, NOT, and maybe XOR. The equivalents in assembly and C (and many other programming languages):
| Operation | Assembly | C |
|---|---|---|
| bitwise-AND | and $1, %rdi | n = n & 1; |
| bitwise-OR | or $1, %rdi | n = n | 1; |
| bitwise-XOR | xor $1, %rdi | n = n ^ 1; |
| bitwise-NOT | not %rdi | n = ~n; |
Bit Fields
Note: be careful not to confuse the bitwise operators (&, |, ~) with the boolean operators (&&, ||, !).
The bitwise operators work on integers (or on 64-bit values that we tend to think of as integers), and the boolean operators work on boolean values (true and false) and do different operations, but because C is so permissive, you can legally use either of them in a if or while condition.
Bit Fields
What we're going to do: store several single-bit (boolean) values in an integer (probably unsigned, but the bits don't care).
Each bit position can hold one of our fields with 1 = on/yes/true and 0 = off/no/false.
Bit Fields
I'll define some compile-time constants for the type (to make it clear which integers are bit fields vs actual integers), and integers with a single bit set for each field we want to store.
#define BIT_FIELD uint8_t #define TALL 0x01 // 00000001 #define SHARP 0x02 // 00000010 #define LOUD 0x04 // 00000100 #define COOL 0x08 // 00001000 #define SHY 0x10 // 00010000
i.e. each record can be tall
or not, sharp
or not, loud
or not, …
Bit Fields
A record with all fields off
is easy enough:
BIT_FIELD record = 0;
We can turn whichever bits we want on
by ORing together the constants:
BIT_FIELD record = SHARP | LOUD;
That will be a value with (only) the sharp
and loud
bits set.
Bit Fields
We can check to see if bits are set with & and one of the constants: we'll get a zero if the bit is zero, and something else otherwise.
If we look at the value
and check to see if the SHARP | LOUDLOUD bit is set, the bitwise-AND will be (expressed as binary and hexadecimal):
0b00000110 0x06
AND 0b00000100 0x04
= 0b00000100 0x04Bit Fields
That implies logic like this to check if a bit is set (recalling that the C if tests for non-zero values):
if ( record & LOUD ) {
printf("is loud\n");
} else {
printf("is not loud\n");
}
(If you put an integer in a C if condition like this, there's an implicit
comparison.)!=0
Bit Fields
If we want to take a bitfield value and set (to 1) a specific bit:
// set the LOUD bit record |= LOUD;
To clear (to 0) a bit:
// clear the LOUD bit record &= ~LOUD;
Bit Fields
record &= ~LOUD;
That last example might deserve more explanation:
LOUD == 0x04 == 0b00000100 ~LOUD == 0b11111011
If we bitwise-AND that with anything, the result will be unchanged, except the LOUD bit will be cleared to 0.
Testing Bits in Assembly
Remember how I said before: the cmp is really just sub, but it throws away the results (and sets the status bits)? That works because comparing differences to zero is useful.
\[ a-b < 0 \quad\Leftrightarrow\quad a < b \\ a-b > 0 \quad\Leftrightarrow\quad a > b \\ a-b = 0 \quad\Leftrightarrow\quad a = b \]
… and the status bits are set for positive/negative/zero after arithmetic operations.
Testing Bits in Assembly
It turns out that the test instruction just does and but throws away the result.
We have always used test like this:
test %rdi, %rdi
… and bitwise-AND-ing anything with itself doesn't change the value. So, the result was comparing the original value (with zero because of the way we look at the status flags).
Testing Bits in Assembly
But we can use test with other operands. If we want to check a bit, we can AND with a single-bit constant, just like in C.
We can define assembly-time constants in GNU Assembler code like this:
.equ TALL, 0x01 .equ SHARP, 0x02 .equ LOUD, 0x04 .equ COOL, 0x08 .equ SHY, 0x10
Testing Bits in Assembly
The equivalent of the is_loud function in assembly:
is_loud:
test $LOUD, %rdi
jz print_not_loud
print_loud:
...
ret
print_not_loud:
...
ret
Testing Bits in Assembly
The equivalent of record = SHARP | LOUD (using %rbx as the variable):
mov $LOUD, %rbx or $SHARP, %rbx
(The compiler can do that at compile-time. We're going to do it at runtime here.)
Testing Bits in Assembly
To clear a bit (data &= ~LOUD):
mov $LOUD, %rax not %rax and %rax, %rbx
To set a bit (data |= LOUD):
or $LOUD, %rbx
(Again, the compiler can do ~LOUD at compile-time.)
Multiplying and Dividing
We observed when first looking at binary: if you add a 0 to the right of a base-10 number, you multiply by 10, and for an unsigned binary (base-2) number, you multiply by 2.
\[ 00001101_2 = 13_{10} \\ 00011010_2 = 26_{10} \]
And in the opposite direction: if you drop a 0, you are dividing by the base.
Multiplying and Dividing
If there's a 1 in the least-significant position of an unsigned binary value, dropping it divides by 2, rounding down (toward \(-\infty\)).
\[ 00011011_2 = 27_{10}\\ 00001101_2 = 13_{10} \]
Multiplying and Dividing
For signed values, it's the same story if we shift everything to the left and fill in a 0:
\[\begin{align*} 11111011_2 &= -5_{10}\\ 11110110_2 &= -10_{10} \end{align*}\]
Multiplying and Dividing
When shifting to the right, we need to sign-extend to fill in the bits for signed values:
\[ 11111011_2 = -5_{10}\\ \boldsymbol{1}1111101_2 = -3_{10} \]
\[ 11111010_2 = -6_{10}\\ \boldsymbol{1}1111101_2 = -3_{10} \]
If we were thinking of these as unsigned values, filling in the left-most bit with 0 would have got the correct result: 251 and 250 would both shift one place right to 125.
Multiplying and Dividing
In general, we can use that shift operation to multiply and divide by powers of two: shifting left \(n\) positions (filling with 0s) is equivalent to multiplying by \(2^n\).
And shifting right (filling with 0s for unsigned, and sign-extending for signed) is equivalent to dividing by \(2^n\) and rounding down.
Multiplying and Dividing
In assembly, the shr (shift right) and shl (shift left) shift unsigned values. The sar (shift-arithmetic right) and sal (shift-arithmetic left) instructions are intended to shift signed values.
They take two operands and can shift by as many places as you like. This multiplies rdi by \(8=2^3\).
shl $3, %rdi
The shift instructions set the CF flag to the first bit shifted out.
Multiplying and Dividing
Or in table form:
| Instr | Action |
|---|---|
shl $2, %rdi | shift left, filling 0s |
sal $2, %rdi | shift left, filling 0s |
shr $2, %rdi | shift right, filling 0s |
sar $2, %rdi | shift right, filling sign bit |
Note: shl and sal are exactly the same instruction (even in machine code) but shr and sar are distinct.
Multiplying and Dividing
This only helps if we're multiplying/dividing by powers of two, but that's common and might be faster. e.g. this multiplies by 33 (\(=2^5+1\)):
mul33:
mov %rdi, %rax
sal $5, %rax # rax = 32 * n
add %rdi, %rax # rax += n
ret
Multiplying and Dividing
This code also multiplies by 33:
mul33:
mov %rdi, %rax
imul $33, %rax
ret
Which is faster? Traditionally, we would assume multiplication is slow and shifting+adding is fast. It's unclear if that's true in modern processors (see lab 5).
Multiplying and Dividing
If you're in anything other than assembly, my advice is to write readable code.
uint64_t mul33(uint64_t n) {
return 33*n;
}
Let the compiler decide what implementation of that logic is faster. [Mine seems to choose the shift+add method for modern x86 processors.]
Example: count set bits
An example where thinking about bitwise operations leads to a surprising algorithm…
The problem: count the number of 1 bits in a binary value. e.g. in a bitfield value, how many of the bits are set? This is known as the value's population count.
Example: count set bits
What I would have done: one iteration for each bit:
uint8_t popcount1(uint64_t n) {
uint8_t count = 0;
while (n > 0) {
if (n % 2 == 1) { // 1 in the 1s place
count += 1;
}
n >>= 1; // shift right 1
}
return count;
}
Example: count set bits
But look what happens if we subtract one from any unsigned integer:
001101001000 - 000000000001 = 001101000111
On the right, we had to borrow until we got a 1: it changes to 0 and 1s fill in to the right. In other words, subtracting one changes all the right-most 0s to 1s, and the first 1 to a 0.
Example: count set bits
Then if we do a bitwise-AND of \(n\) and \(n-1\):
n = 001101001000 n-1 = 001101000111 n & (n-1) = 001101000000
So, n & (n-1) is n but with the lowest-set bit cleared.
Example: count set bits
Spontaneous example of the (n-1) & n operation and binary subtraction:
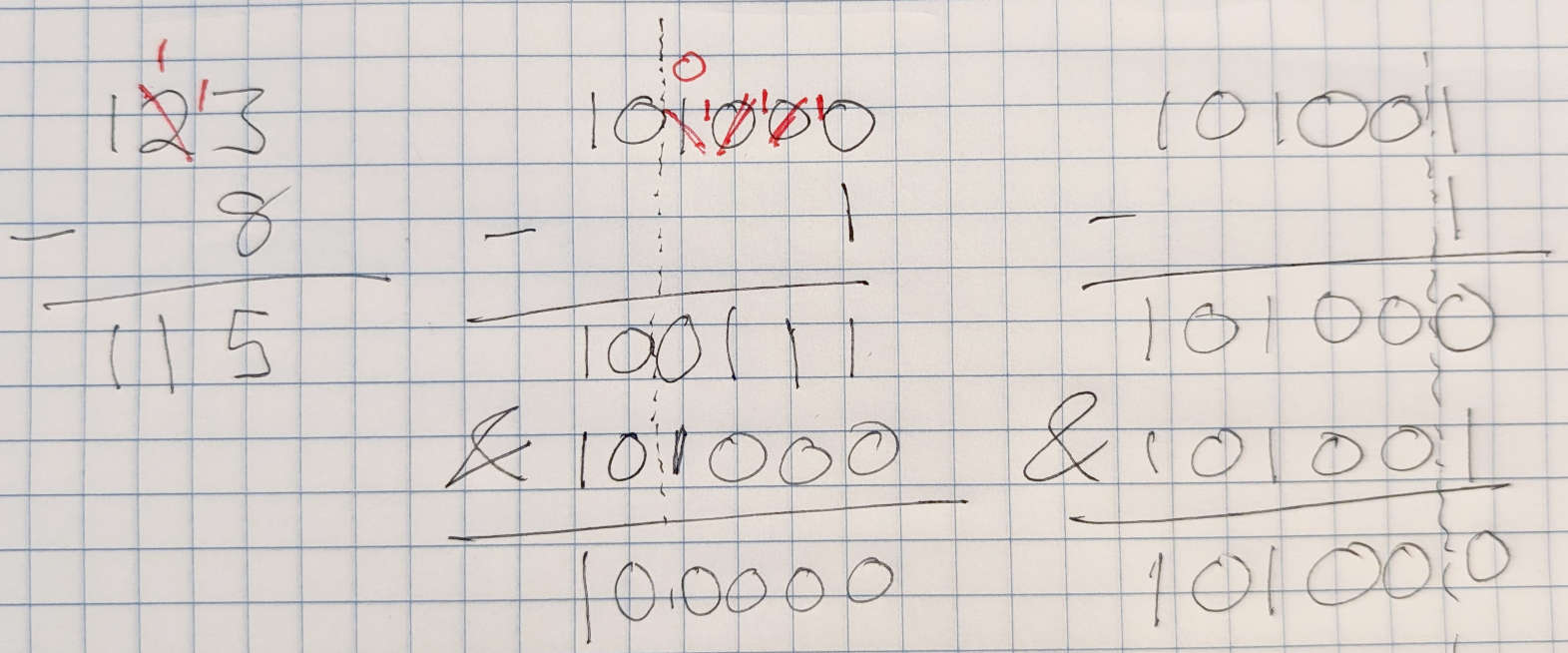
Example: count set bits
That leads to an algorithm (credited to Brian Kernighan) that also counts the set bits, but with one iteration per set bit, and no if [later topic: “branch predictor”]:
uint8_t popcount2(uint64_t n) {
uint8_t count = 0;
while (n > 0) {
count += 1;
n &= n - 1; // clear the lowest set bit
}
return count;
}
Example: count set bits
There are other algorithms for population count, which are also fun.
It turns out, it's a common enough operation (and/or easy enough to build a circuit for) that there's an x86-64 instruction for it (after ≈2008), and a way to ask for it (or a fallback implementation) in C:
popcount:
popcnt %rdi, %rax
uint8_t popcount3(uint64_t n) {
return (uint8_t)__builtin_popcountll(n);
}
Example: count set bits
The lesson, again: thinking in bits can lead to surprising algorithms. Knowing your processor helps too.